本题是2020年第三届安洵杯的一个题目,当时也是我当时费了好长时间时间才做出来的一个题,题目对AES-CBC的加密流程考察的很清晰
Task:
#!/usr/bin/python
from Crypto.Cipher import AES
import binascii
from Crypto.Util.number import bytes_to_long
from flag import flag
import random
import string
import os
def genkey(l):
return random.getrandbits(l)
iv = flag.strip(b'flag{').strip(b'}')
key = ''.join([random.choice(string.ascii_letters+string.digits) for _ in xrange(16)])
LENGTH = len(key)
assert LENGTH == 16
hint = os.urandom(4) * 8
print(bytes_to_long(hint)^bytes_to_long(key))
msg = b'Welcome, ctfer. Dont try too hard, its no use. Have a good day!!'
def encrypto(message):
aes = AES.new(key,AES.MODE_CBC,iv)
return aes.encrypt(message)
print(binascii.hexlify(encrypto(msg))[-32:])
'''
99748265546679089946917295913637945222843938798184123305418691873367322323659
bc03f3ac4ff8064acbcfaf0b0bf2ba7b
'''
0x10 题目分析以及加密流程分析
在完成题目之前,我们要先学习什么是AES-CBC, 以及他的加密解密流程
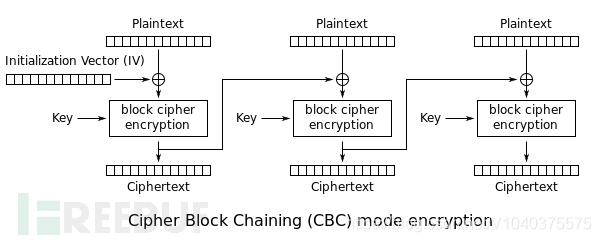
Plaintext:明文数据
IV:初始向量
Key:分组加密使用的密钥
Ciphertext:密文数据
明文都是先与混淆数据(第一组是与IV,之后都是与前一组的密文)进行异或,再执行分组加密的。
1、首先将明文分组(常见的以16字节为一组),位数不足的使用特殊字符填充。
2、生成一个随机的初始化向量(IV)和一个密钥。
3、将IV和第一组明文异或。
4、用密钥对3中xor后产生的密文加密。
5、用4中产生的密文对第二组明文进行xor操作。
6、用密钥对5中产生的密文加密。
7、重复4-7,到最后一组明文。
8、将IV和加密后的密文拼接在一起,得到最终的密文。
解密过程:
每组解密时,先进行分组加密算法的解密,然后与前一组的密文进行异或才是最初的明文。
对于第一组则是与IV进行异或。
1、从密文中提取出IV,然后将密文分组。
2、使用密钥对第一组的密文解密,然后和IV进行xor得到明文。
3、使用密钥对第二组密文解密,然后和2中的密文xor得到明文。
4、重复2-3,直到最后一组密文。
根据这个加密流程我们可以得到
假设aes 加密函数为enc(msg,key),初始向量为iv,key = key, 则其加密流程大致为:
enc1 = enc(msg[0]^ iv ,key)
enc2 = enc(msg[1]^enc(msg[0]^ iv ,key),key)
enc3 = enc(msg[2]^enc(msg[1]^enc(msg[0]^ iv ,key),key),key)
enc4 = enc(msg[3]^enc(msg[2]^enc(msg[1]^enc(msg[0]^ iv ,key),key),key),key)
final_enc = enc1+enc2+enc3+enc4
而由于题目中所给出的hint长度与key长度不一样,导致我们可以推出hint,从而恢复出key
tmp = 99748265546679089946917295913637945222843938798184123305418691873367322323659
hint = int(str(hex(tmp))[2:10] * 8,16)
key = long_to_bytes(tmp ^ hint)
而此时我们已经有的信息包括
enc4
key
msg[0],msg[1],msg[2],msg[3]
我们要通过这些已知量求出初始向量
解密图:
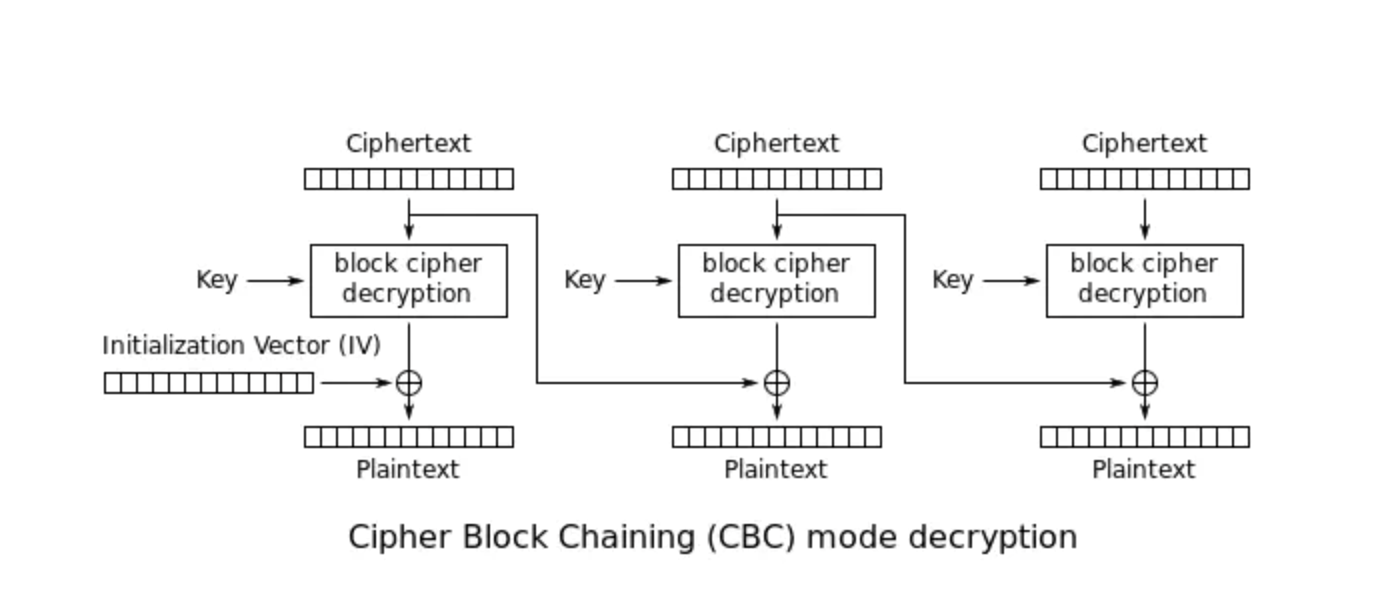
假设aes 解密函数为decrypt(enc,key),初始向量为iv,key = key, 则其解密流程大致为:
msg[0] = decrypt(enc1,key)^iv
msg[1] = decrypt(enc2,key)^enc1
msg[2] = decrypt(enc3,key)^enc2
msg[3] = decrypt(enc4,key)^enc3
msg = msg[0]+msg[1]+msg[2]+msg[3]
而我们已经有enc4,key,msg[0],msg[1],msg[2],msg[3],因此:
enc3 = decrypt(enc4,key)^msg[3]
enc2 = decrypt(enc3,key)^msg[2]
enc1 = decrypt(enc2,key)^msg[1]
iv = decrypt(enc1,key)^msg[0]
从而恢复出初始向量
0x20 POC
#!/usr/bin/python
from Crypto.Util.number import long_to_bytes
import binascii, sys
from Crypto.Util.strxor import strxor
from Crypto.Cipher import AES
# -----------get key---------
tmp = 99748265546679089946917295913637945222843938798184123305418691873367322323659
hint = int(str(hex(tmp))[2:10] * 8,16)
key = long_to_bytes(tmp ^ hint)
# ----------get iv-----------
msg = b'Welcome, ctfer. Dont try too hard, its no use. Have a good day!!'
msgs = [msg[ii:(ii+16)] for ii in range(0,len(msg),16)]
print msgs
msgs.reverse()
IV = binascii.unhexlify('bc03f3ac4ff8064acbcfaf0b0bf2ba7b')
def decry(key,IV,ms):
aes=AES.new(key,AES.MODE_ECB)
return strxor(aes.decrypt(IV),ms)
for ms in msgs:
IV=decry(key,IV,ms)
print(b'flag{' + IV+ b'}')
