RSA 入门基础
0x00 数学基础
素数(质数)、合数、互质数
素数:
一个数如果除了1与它本身之外没有其他的因数,那么这个数就被称为素数(或者质数,取自英文单词prime的首字母)
合数:
如果一个数大于1,且该数本身不是素数,那么这个数就是一个合数。
互质数:
如果两个整数𝑎,𝑏a,b的最大公因数(greatest common divisor)为1,即𝑔𝑐d(𝑎,𝑏)=1gcd(a,b)=1,那么称a,b两数互质,。
模反元素:
如果两个正整数e和n互质,那么一定可以找到整数d,使得
e * (d -1)被𝑛n整除,或者说e * d被𝑛n除的余数是1。这时,𝑑d就叫做𝑒e的“模反元素”。欧拉定理可以用来证明模反元素必然存在。两个整数𝑎,𝑏a,b,它们除以整数𝑀M所得的余数相等:a ≡ b ( mod m),比如说5除3余数为2,11除3余数也为2,于是可写成11 ≡ 5 ( mod 3)
0x10 常见题型
-
以及N,e,且N可被工具分解,求D
-
已知dp ,e ,n ,c 求m
-
Winer attack e很大的那种 diffwiner等
-
e很小
-
共模攻击
-
dp高位泄漏
分解N方法:
- Pollard-Rho
- yafu
- factordb
- Coppersmith
0x20 RSA test
from Crypto.Util.number import getPrime, bytes_to_long ,long_to_bytes
from gmpy2 import *
m = "RSA_test!!"
m = bytes_to_long(m)
print m
p = getPrime(256)
q = getPrime(256)
print len(bin(p)[2:])
n = p*q
print len(bin(n)[2:])
e = 0x10001
c = powmod(m,e,n) # m^e % n = c
print c
ph = (p-1)*(q-1)
d = invert(e,ph)
print d
m = powmod(c,d,n)
print m
print long_to_bytes(m)
# p q e ,d
# n, e c, m
# 4 = 1*4 2*2
# 12414234131321321414314134241341
0x30 Cute RSA
考点:最大公约数来分解N
Rabbit 解密
特征:给了两个N
task
from Crypto.Util.number import getPrime, bytes_to_long
from gmpy2 import *
def getN():
p = getPrime(256)
q = getPrime(256)
r = getPrime(256)
return p*q, q*r
if __name__ == '__main__':
flag = ""
N1, N2 = getN()
e = 0x10001
print "N1 = ",N1
print "N2 = ",N2
m = bytes_to_long(flag)
c = powmod(m,e,N1)
print "C = ", c
"""
N1 = 8690082378724956131728693549405680920898741763481248428044836622842273931157442286952744403209742927421806913694338426401096833093631524281214826492157171
N2 = 8943208835357819241220295088579135787736447047617211073968349918722104246067900127013910964113505400479265498046601286733092361702205069453201849816540051
C = 2211363752558817846076244655241271727941483995375152985045401048763346362430115884897972330650265905224940073753211446339656874861126590073417989725002422
"""
解题:
from Crypto.Util.number import getPrime, bytes_to_long, long_to_bytes
from gmpy2 import *
N1 = 8690082378724956131728693549405680920898741763481248428044836622842273931157442286952744403209742927421806913694338426401096833093631524281214826492157171
N2 = 8943208835357819241220295088579135787736447047617211073968349918722104246067900127013910964113505400479265498046601286733092361702205069453201849816540051
C = 2211363752558817846076244655241271727941483995375152985045401048763346362430115884897972330650265905224940073753211446339656874861126590073417989725002422
e = 0x10001
p = gcd(N1,N2)
q = N1 // p
ph_n = (p-1)*(q-1)
d = invert(e,ph_n)
m = powmod(C,d,N1)
print long_to_bytes(m)
0x40 easy rsa
共模攻击
Task
from Crypto.Util.number import getPrime, bytes_to_long ,long_to_bytes
from gmpy2 import *
flag = "flag{RSA_attack_Common_mode!}"
p = getPrime(256)
q = getPrime(256)
e1 = 0x10001
e2 = 0x5001
N = p*q
m = bytes_to_long(flag)
C1 = powmod(m,e1,N)
C2 = powmod(m,e2,N)
print "C1: ", C1
print "C2: ", C2
print "e1: ", e1
print "e2: ", e2
print "N: ", N
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
g, x, y = egcd(a, m)
if g != 1:
raise Exception('modular inverse does not exist')
else:
return x % m
s = egcd(e1, e2)
s1 = s[1]
s2 = s[2]
if s1 < 0:
s1 = - s1
C1 = modinv(C1, N)
elif s2 < 0:
s2 = - s2
C2 = modinv(C2, N)
m = (C1**s1)*(C2**s2) % N
print(long_to_bytes(m))
0x50 winer
Winer attack
task
from Crypto.Util.number import getPrime, bytes_to_long ,long_to_bytes
from gmpy2 import *
flag = "flag{Wow_welcome_here!}"
n = 0x92411fa0c93c1b27f89e436d8c4698bcf554938396803a5b62bd10c9bfcbf85a483bd87bb2d6a8dc00c32d8a7caf30d8899d90cb8f5838cae95f7ff5358847db1244006c140edfcc36adbdcaa16cd27432b4d50d2348b5c15c209364d7914ef50425e4c3da07612cc34e9b93b98d394b43f3eb0a5a806c70f06697b6189606eb9707104a7b6ff059011bac957e2aae9ec406a4ff8f8062400d2312a207a9e018f4b4e961c943dfc410a26828d2e88b24e4100162228a5bbf0824cf2f1c8e7b915efa385efeb505a9746e5d19967766618007ddf0d99525e9a41997217484d64c6a879d762098b9807bee46a219be76941b9ff31465463981e230eecec69691d1
e = 0x6f6b385dd0f06043c20a7d8e5920802265e1baab9d692e7c20b69391cc5635dbcaae59726ec5882f168b3a292bd52c976533d3ad498b7f561c3dc01a76597e47cfe60614f247551b3dbe200e2196eaa001a1d183886eeacddfe82d80b38aea24de1a337177683ed802942827ce4d28e20efef92f38f1b1a18c66f9b45f5148cceabfd736de8ac4a49e63a8d35a83b664f9f3b00f822b6f11ff13257ee6e0c00ca5c98e661ea594a9e66f2bd56b33d9a13f5c997e67a37fcf9a0c7f04d119fe1ba261127357e64a4b069aefed3049c1c1fe4f964fd078b88bedd064abea385cfebd65e563f93c12d34eb6426e8aa321033cfd8fe8855b9e74d07fe4f9d70de46f
m = bytes_to_long(flag)
d = getPrime(128)
c = powmod(m,e,n)
print "c = ", c
print "n = ", n
print "e = ", e
# m^e % n = c , e加密指数
# c ^ d %n = m d 解密指数
解密
# -*- coding: utf-8 -*-
import gmpy2
import time
# 展开为连分数
def continuedFra(x, y):
cF = []
while y:
cF += [x / y]
x, y = y, x % y
return cF
def Simplify(ctnf):
numerator = 0
denominator = 1
for x in ctnf[::-1]:
numerator, denominator = denominator, x * denominator + numerator
return (numerator, denominator)
# 连分数化简
def calculateFrac(x, y):
cF = continuedFra(x, y)
cF = map(Simplify, (cF[0:i] for i in xrange(1, len(cF))))
return cF
# 解韦达定理
def solve_pq(a, b, c):
par = gmpy2.isqrt(b * b - 4 * a * c)
return (-b + par) / (2 * a), (-b - par) / (2 * a)
def wienerAttack(e, n):
for (d, k) in calculateFrac(e, n):
if k == 0: continue
if (e * d - 1) % k != 0: continue
phi = (e * d - 1) / k
p, q = solve_pq(1, n - phi + 1, n)
if p * q == n:
return abs(int(p)), abs(int(q))
print 'not find!'
time.clock()
n = 0x92411fa0c93c1b27f89e436d8c4698bcf554938396803a5b62bd10c9bfcbf85a483bd87bb2d6a8dc00c32d8a7caf30d8899d90cb8f5838cae95f7ff5358847db1244006c140edfcc36adbdcaa16cd27432b4d50d2348b5c15c209364d7914ef50425e4c3da07612cc34e9b93b98d394b43f3eb0a5a806c70f06697b6189606eb9707104a7b6ff059011bac957e2aae9ec406a4ff8f8062400d2312a207a9e018f4b4e961c943dfc410a26828d2e88b24e4100162228a5bbf0824cf2f1c8e7b915efa385efeb505a9746e5d19967766618007ddf0d99525e9a41997217484d64c6a879d762098b9807bee46a219be76941b9ff31465463981e230eecec69691d1
e = 0x6f6b385dd0f06043c20a7d8e5920802265e1baab9d692e7c20b69391cc5635dbcaae59726ec5882f168b3a292bd52c976533d3ad498b7f561c3dc01a76597e47cfe60614f247551b3dbe200e2196eaa001a1d183886eeacddfe82d80b38aea24de1a337177683ed802942827ce4d28e20efef92f38f1b1a18c66f9b45f5148cceabfd736de8ac4a49e63a8d35a83b664f9f3b00f822b6f11ff13257ee6e0c00ca5c98e661ea594a9e66f2bd56b33d9a13f5c997e67a37fcf9a0c7f04d119fe1ba261127357e64a4b069aefed3049c1c1fe4f964fd078b88bedd064abea385cfebd65e563f93c12d34eb6426e8aa321033cfd8fe8855b9e74d07fe4f9d70de46f
c = 8182643108113711551719741770359737427132160178317160256646779627961786011836412574906951692979551231647117033579808452196148029416594613738969370327072289432199135565450376698136381548415941180998733651675736619159455480096030614352212813680858385021388645155026545798817750931180139746649840496610076633000499655316226880120200144647540225359556920626890519801594482041607179092936768787605351213175531356975620870684482757784189733651663505439484193062338395860909703419095153858484501183168723583042399424350632786942936810939486992835312705917848638156559400132510487149420324006490558184306457491599733731346130
print('e',e,'n',n)
p, q = wienerAttack(e, n)
print '[+]Found!'
print ' [-]p =',p
print ' [-]q =',q
print ' [-]n =',p*q
d = gmpy2.invert(e,(p-1)*(q-1))
print ' [-]d =', d
print ' [-]m is:' + '{:x}'.format(pow(c,d,n)).decode('hex')
print '\n[!]Timer:', round(time.clock(),2), 's'
print '[!]All Done!'
0x60 DP O DP
dp泄漏
task
from Crypto.Util.number import getPrime, bytes_to_long ,long_to_bytes
from gmpy2 import *
flag = "flag{dp_yyds!!!!!!!!!!!!!!dp}"
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 0x10001
m = bytes_to_long(flag)
c = powmod(m,e,n)
ph = (p-1)*(q-1)
d = invert(e,ph)
dp = d % (p-1)
print "N: ", n
print "C: ", c
print "e: ", e
print "dp: ", dp
def getd(n,e,dp):
for i in range(1,e):
if (dp*e-1)%i == 0:
if n%(((dp*e-1)/i)+1)==0:
p=((dp*e-1)/i)+1
q=n/(((dp*e-1)/i)+1)
phi = (p-1)*(q-1)
d = invert(e,phi)%phi
return d
d = getd(n,e,dp)
m = powmod(c,d,n)
print long_to_bytes(m)
0x70 双子座
考点:孪生素数
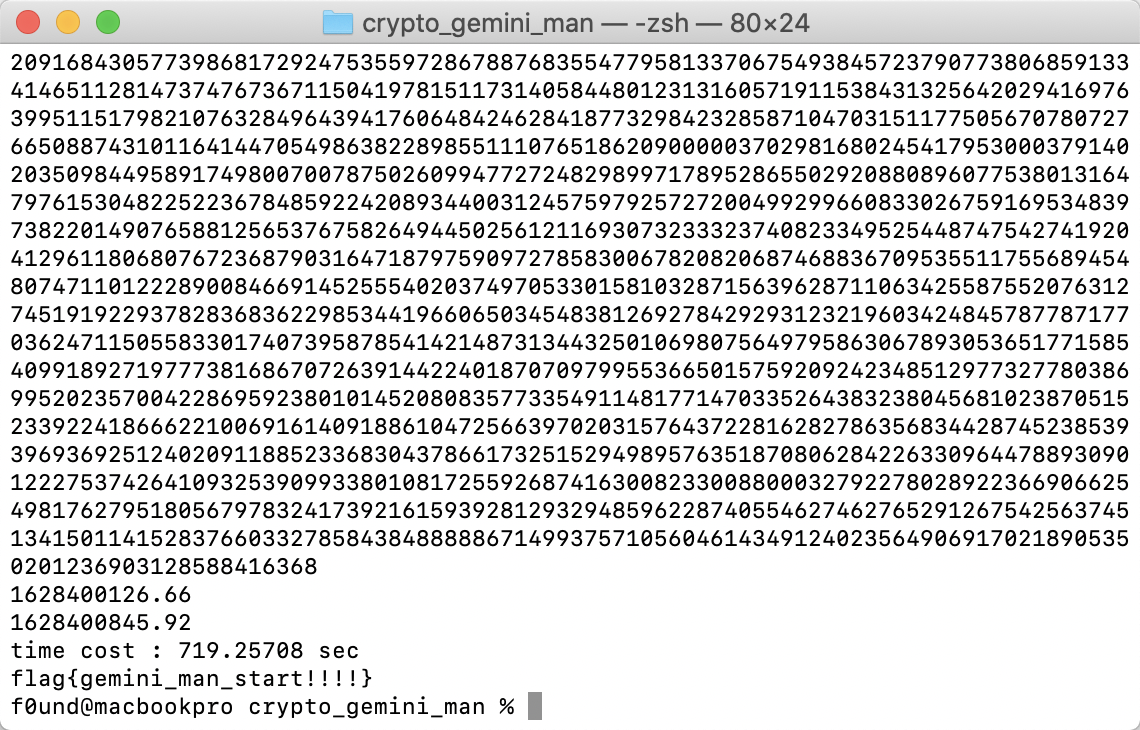
task
from Crypto.Util.number import getPrime, bytes_to_long ,long_to_bytes
from gmpy2 import *
import time
flag = "flag{gemini_man_start!!!!}"
N = int(open("N.txt").read())
m = bytes_to_long(flag)
e = 0x10001
c = powmod(m,e,N)
print c
p = iroot(N,2)[0]
q = p+2
assert(p*q == N)
n = p*q
ph = (p-1)*(q-1)
d = invert(e,ph)
start = time.time()
print start
m = powmod(c,d,n)
end = time.time()
print end
running_time = end-start
print('time cost : %.5f sec' %running_time)
print(long_to_bytes(m))
